Donor Lotteries In Depth

Why a donor lottery?

Donating effectively is a tough problem. Finding highly effective organisations is a time-consuming, resource-intensive job. Large foundations (such as Open Philanthropy or the Gates Foundation) spend a significant amount of time researching these questions, but for individual donors, making these decisions can be hard. Furthermore, given the size of any individual donor’s donation, it’s often hard for each person to justify investing a lot of time into investigating the most effective use of their money.

For these reasons we often recommend donors give to expert-led grantmaking funds or follow the advice of trusted charity evaluators. But choosing which funds or evaluators to rely on is also a difficult task, and it may be the case that there is no relevant expert who you believe captures all the considerations.

Another option we recommend for some donors is to participate in a donor lottery. Donor lotteries give donors a stake in directing a larger pot of money than they’d typically decide on just by themselves. Each donor’s probability of winning the lottery is proportional to their donation, and the winner can spend time thinking and researching their decision and then recommend grants for the whole pot. In expectation, each donor is granting the same amount of money to their preferred charities as they would have if they had donated directly. However, for the donor that wins, the larger pot of money makes it worthwhile to spend more time and energy researching where the money should go. It also creates an economy of scale for the other individual donors in the lottery, as only one person is required to do the research, and gets around situations where a donor would like to give to an organisation with a minimum donation size.

For more information on the genesis of the donor lottery, we recommend reading Carl Shulman’s post introducing the idea of donor lotteries or EA Fund’s post explaining why contributing to a donor lottery might be an especially impactful way to give.

Donate to Donor Lottery

Dates

There are three significant dates in the Giving What We Can Donor Lottery:

• Close date: When new entries into the lottery stop being accepted (you can only enter a lottery before the close date).
• Lock date: When all payments must be finalised and when lottery entrants will receive their ticket numbers.
• Draw date: When the lottery will be drawn. The UNIX timestamp of this date will be used to select the NIST beacon entry from which the winning lottery number is derived.

How it works

Entering the lottery

• Entries must be made by making a donation to the Donor Lottery before the close date.
• To enter the lottery click ‘Enter lottery’ on one of the open donor lotteries on the Donor Lottery page before the relevant close date.
• Once you have made a donation using the payment form, you will be entered into the lottery and your entry will show up on the details page for that lottery.
• When you enter, you will receive an email confirming your entry, probability of winning, and the lock time and draw time of the lottery.
• You can choose to publicly display your name against your lottery entry, or to remain anonymous.
• Lottery winners will be encouraged to provide a write up on how they arrived at their allocation decision (which Giving What We Can can publish on behalf of the winner, if the winner wishes to remain anonymous).
• The winner's grant recommendations will be made public regardless of whether the winner remains anonymous or whether they provide a write up.

Tax Deductibility and Gift Aid

• Tax Benefits: Your contributions to the Donor Lottery are eligible for the same tax benefits as other donations made through our platform. During the payment process, simply select your country, and we'll provide you with the information you need for tax benefits applicable to your country.
• Tax Receipts: Once your donation is confirmed, a tax receipt will be immediately generated for you. You can use this for tax purposes.
• Timing: The date on the tax receipt corresponds to the date the payment was made, not the lottery closing or draw dates.

Blocks

• Defining Block Size: Each lottery is structured around a 'block size', which is a predetermined amount of funds that make up the lottery pot. This size is guaranteed by a dedicated benefactor.
• Benefactor's Role: The benefactor serves as a backstop, ensuring the lottery pot will reach at least the size of the predetermined block.
• Exceeding the Block Size: If the total donations surpass the initial block size, a new block is formed. This ensures that your odds of winning—calculated as your donation amount divided by the block size—remain constant.

Winning

• Ticket Assignment: Upon entering, each participant receives a 'ticket', which represents a range of numbers within the block.
• Winning Number: The participant holding the ticket range that the winning number falls within will be declared the winner.
• Unallocated Ranges: Any number ranges that remain unallocated are designated to the lottery guarantor, our backstopping benefactor.

Reports from past lottery winners

Learn more about how previous donor lotteries (run by us or by others) have been distributed by reading these donor lottery reports:

• 2018-2019 Donor Lottery (part 1 and part 2) by Ross Rheingans-Yoo
• 2017-2018 Donor Lottery by Adam Gleave
• 2016-2017 Donor Lottery by Timothy Telleen-Lawton

Terms, Conditions, and Caveats

• Net Amount: If you choose a payment method with associated fees (e.g. credit/debit cards or GoCardless), your entry into the lottery will be based on the amount remaining after these fees are deducted.
• Gift Aid: For UK donors that are eligible for Gift Aid your entry will be based on your donation amount, minus any fees, plus an additional 25% claimed through Gift Aid. We require that you provide us with the correct information needed to claim the Gift Aid.
• Currency: All lottery activities are denominated in USD. If you donate in a different currency, we'll convert your donation into USD using recent exchange rates, courtesy of Open Exchange Rates.
• Administration: The Donor Lottery is administered by Giving What We Can UK and Giving What We Can USA Inc.
• Discretionary Grants: Please note that our funding partners have the final say in all grantmaking decisions.
• Grantee Limitations: Our funding partners can only make grants that fall within their defined charitable objects and are compliant with tax laws in their registered countries. Generally, any program listed on Giving What We Can, as well as most other registered non-profits in several jurisdictions, should be eligible for grants. Special cases will be evaluated individually. If a recommendation cannot be followed, the winner will be given the opportunity to suggest an alternative. Should you have any questions about the eligibility of a potential grantee, please get in touch before entering the lottery.

Further Questions

If you have any questions please get in touch.

Technical details

Entering the lottery

Donors enter the lottery by making a donation to it. The odds of winning are given by the size of the donation relative to the lottery’s block size.

For example, if the block size is $100,000, and you enter the lottery with a $2,000 donation, your probability of winning will be 2%:

2,000 / 100,000 = 0.02

Choosing a winning number

Winners will be selected by taking the first 10 hexadecimal digits of the value of the NIST Randomness Beacon at the lottery’s draw date. The entrant whose ‘ticket’ (see below) contains the winning number will be declared the winner. If there is more than one block, all blocks will use the same winning number. The NIST Beacon provides a publicly-verifiable source of randomness. Links to each block’s NIST beacon entry will be posted on the Lock Date.

Taking the first 10 hexadecimal digits means winning lottery draws will be in the range [0, (16^10 - 1)].

For example, let’s say a lottery's draw date is at midday on December 1, 2017 (UTC). The NIST Beacon value for this time (given by the Unix Timestamp 1512129600) was:

Taking the first ten hexadecimal digits gives us 02FDF3FCCE (or 12850560206 in decimal).

Tickets

Entrants will be assigned a ‘ticket’, which is an interval in the range [0, (16^10-1)].

The size of the interval is given by:

⌊(Probability of winning) * (16^10 - 1)⌋ where ⌊n⌋ = floor(n)

The actual start and end values of a given entrant’s ticket interval will be determined by distributing these intervals across the entire range.

For example, let’s say there are three entrants into a lottery with a block size of $100,000:

• Alice donates $20,000
• Bob donates $10,000
• Carol donates $30,000

The entrants’ ticket sizes are as follows: ``` Range 'R' = (16^10 - 1)
= 1099511627775

Alice ticket size =⌊(20,000 / 100,000) * R⌋
= 219902325555

Bob ticket size = ⌊(10,000 / 100,000) * R⌋
= 109951162777

Carol ticket size = ⌊(30,000 / 100,000) * R⌋
= 329853488332
```

Tickets are allocated by dividing up the entire range of possible winning numbers:

Alice = [ 0, 219902325554] Bob = [219902325555, 329853488331] Carol = [329853488332, 659706976664] Unallocated = [659706976665, 1099511627775] (lottery guarantor)

Represented visually, this looks like (G is the lottery guarantor):

Taking the winning number from above, 12850560206, we declare Alice the winner, as 12850560206 falls within her interval [0, 219902325554].

Multiple blocks

If the lottery takes more in donations than the block size, we split the range into multiple blocks. Multiple blocks ensure that there is no cap on the number of donors who may enter the lottery, while ensuring that the guarantor's liability is capped at the block size.

Let's say that a fourth donor, Dave, enters the lottery before it closes, with a $50,000 donation. As this will overflow the block, a second block is now in play. Dave now has a ticket range that covers $40,000 in the first block, and an additional $10,000 in the second. Note that Dave's chance of winning is still 50%, and as there is only one winning number, he can only win in one of the blocks.

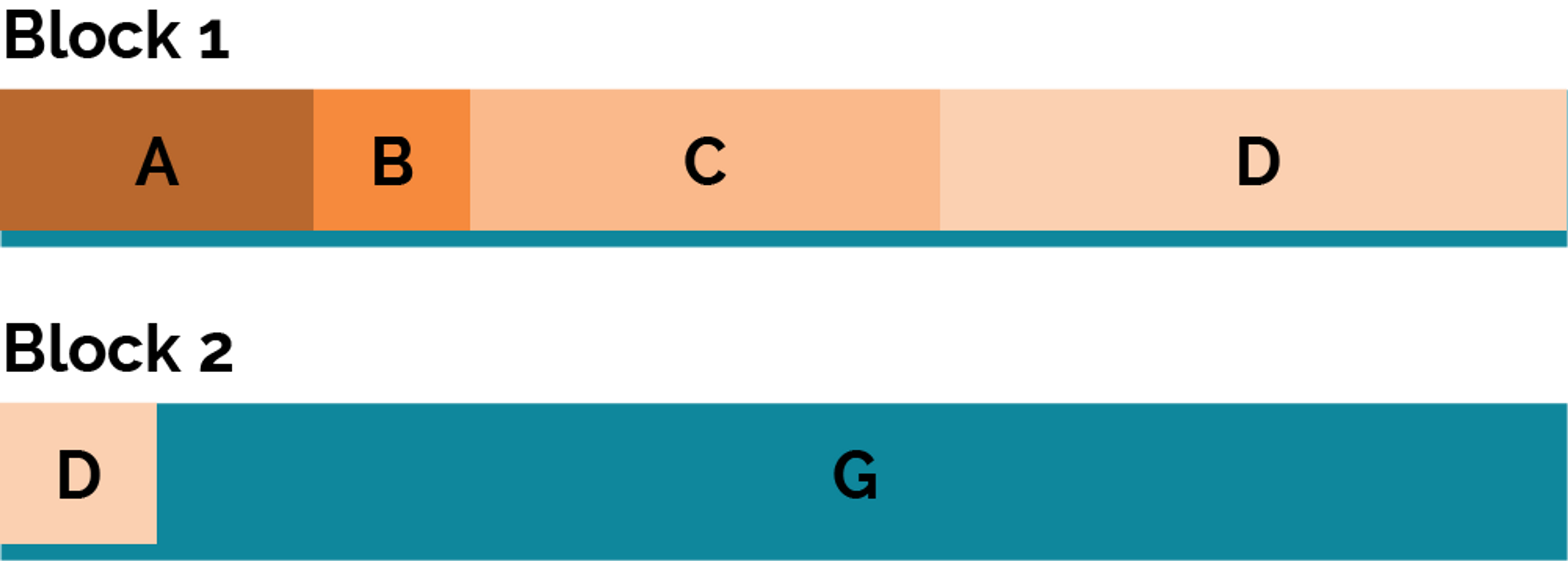
At draw time, winners are selected in each block. Using the same winning number as in the first example, Alice wins the first block, and Dave wins the second. They each may independently recommend $100,000 worth of grants.

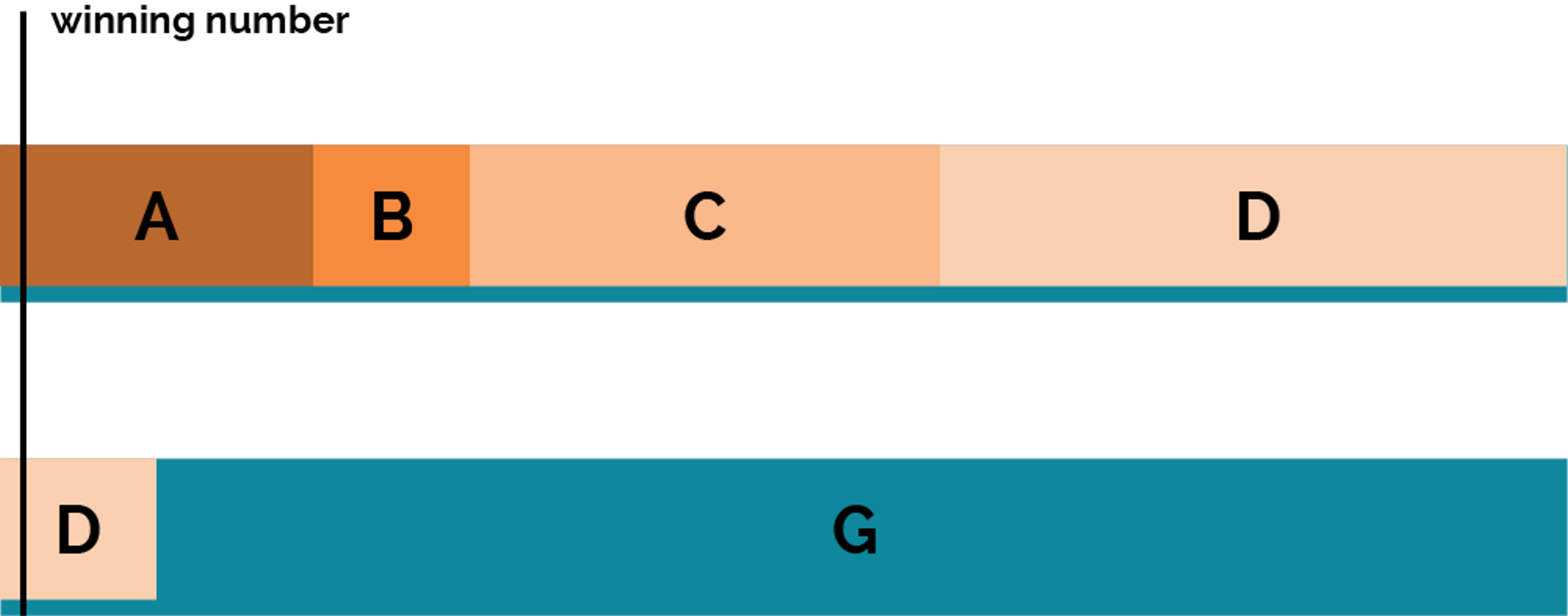
Ticket intervals will be assigned to donors at the lock date of the lottery.